Quick Sort- An Illustrative Tutorial

Introduction to Quick Sort

Quick Sort is a divide-and-conquer sorting algorithm:

• Divide: Pick a pivot and split the array so items smaller than the pivot go to the left, items larger to the right.
• Conquer: Recursively sort both sides.
• Combine: Lists get merged as they are sorted in-place.

Why should you care?

• It’s fast (O(nlogn) average), used in real-world applications- system libraries, and teaches recursion/divide-and-conquer.

How Does Quick Sort Work?

Let’s see it step by step with this array:

Example Array:
44, 33, 11, 55, 77, 90, 40, 60, 99, 22, 88, 66

Step 1. Choose a Pivot

Let’s use the first element: 44.

Step 2. Partition

Rearrange so everything ≤44 is left, >44 is right.

• Which numbers will be on the left of 44 after partitioning?
  • A) 33
  • B) 90
  • C) 22
  • D) 77
    (Answer: A and C)

After partitioning, the array might look like:
33, 11, 22, 40, 44, 90, 77, 60, 99, 55, 88, 66

Pivot 44 is now where it belongs.

Step 3. Recur on both sides

Apply the same process to the left and right sides.

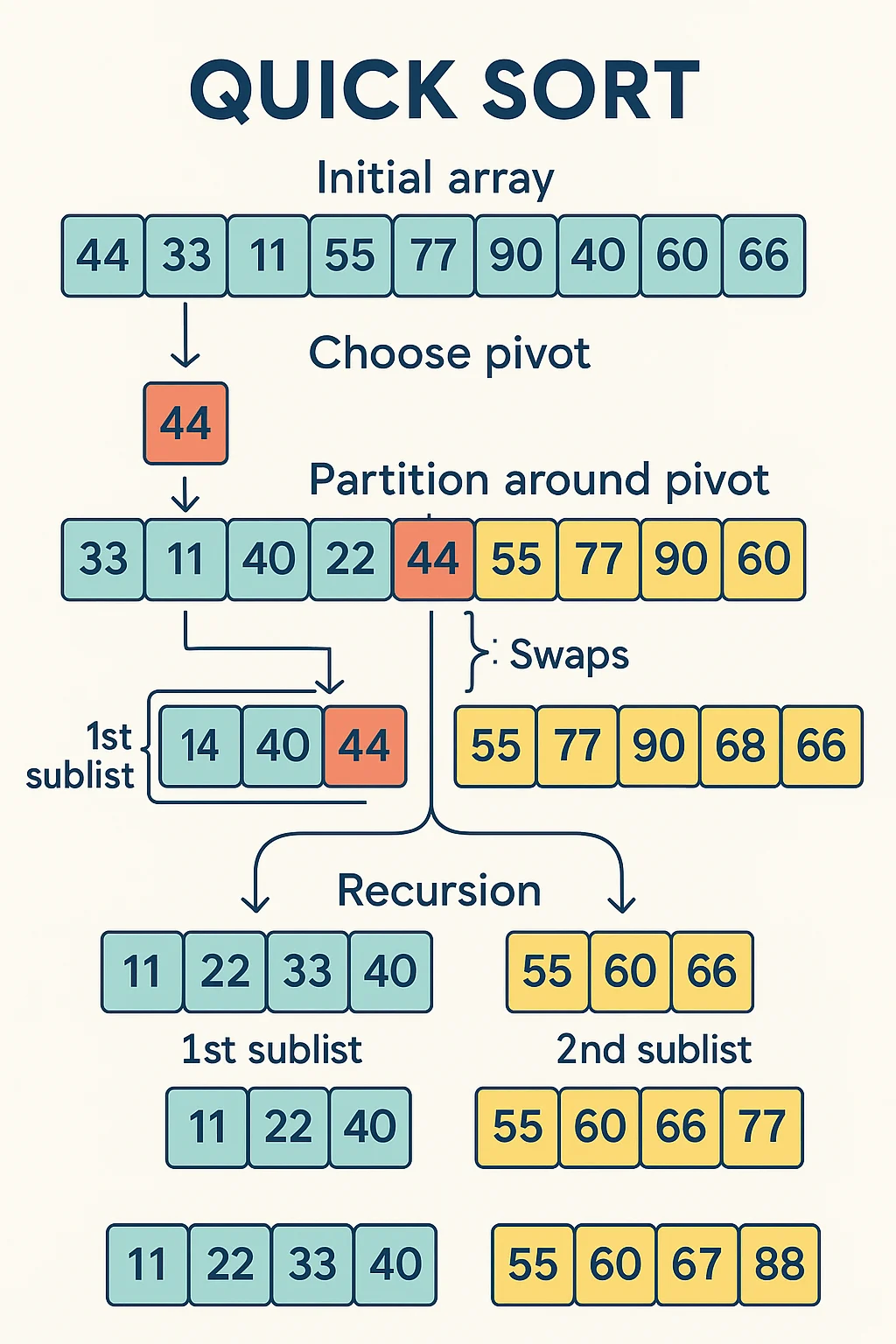
Can you trace what happens next?

Quick Sort Pseudo Code

procedure QuickSort(A, l, u)
    if l < u then
        k ← partition(A, l, u)
        QuickSort(A, l, k - 1)
        QuickSort(A, k + 1, u)
    end if
end procedure

procedure partition(A, l, u)
    pivot ← A[l]
    i ← l + 1
    j ← u
    repeat
        while i ≤ u and A[i] ≤ pivot do
            i ← i + 1
        end while
        while j ≥ l and A[j] > pivot do
            j ← j - 1
        end while
        if i < j then
            swap A[i] and A[j]
        end if
    until i ≥ j
    swap A[l] and A[j]
    return j
end procedure

Try tracing this with the sample numbers above!

Suppose the pick and swap process is:

44, 33, 11, 55, 77, 90, 40, 60, 99, 22, 88, 66
→
33, 11, 22, 40, 44, 90, 77, 60, 99, 55, 88, 66 (pivot 44 in correct spot)

Left subset: 33, 11, 22, 40
Right subset: 90, 77, 60, 99, 55, 88, 66

Keep applying quick sort recursively!

Interactive Quick Sort Demo

Analysis

Worst Case: O(n²) (when the pivot always leads to the most unbalanced split, e.g., already sorted data).
Best and Average Case: O(nlogn) (random pivots, or well-balanced splits).

Recurrence Relation (from notes):

• Worst: T(n) = T(n-1) + O(n)
• Average: T(n) ≤ 2T(n/2) + O(n)

Apply Master Theorem: Average is O(nlogn).

Space Complexity: O(log n) (recursion stack)

Quick Summary Table

Try It Yourself: Self-Check

Given: 44, 33, 11, 55, 77, 90, 40, 60, 99, 22, 88, 66

• What’s the pivot on first pass?
• What’s the array after the pass?
• How does the process continue?

Real-World Applications

Quick sort is essential for:

• Sorting databases
• System libraries (C’s qsort, Python’s .sort uses Timsort—a hybrid which leverages quick sort ideas)
• Any large dataset that needs efficient, in-place sorting

Read more

Do Linked Lists still Matter? – tectrails.com

Top AI Courses to Elevate Your Career in 2025 – tectrails.com

Please leave this field empty

Oh hi there 👋
It’s nice to meet you.

Sign up to receive awesome content in your inbox, every month.

We don’t spam! Read our privacy policy for more info.

Check your inbox or spam folder to confirm your subscription.